|
Triangulacni mereni
Cache je venovana byvale triangulacni vezi na Padaku.
|
|
Na vrcholku kopce, na kterem stojite, kdysi stavala triangulacni vez, podobna te na obrazku. Z ni byl vyhled na okolni veze.
|
 |
|
V trigonometrii a elementární geometrii je triangulace zpusob zjištování souradnic a vzdáleností. Provádí se trigonometrickým výpoctem. Sestrojí se pomyslný trojúhelník, jehož jedna strana je strana již známého jiného trojúhelníku s dvema koncovými referencními body a tretím bodem je místo, jehož souradnice se zjištuje. Triangulace se nejcasteji užívá pro úcely geodézie, navigace, metrologie, astrometrie nebo pri rízení palby.
Tolik z wikipedie.
|
|
...Pomocí techto jednoduchych prostredku (obcansky prukaz ma rozmery 10.5x7.4 cm, prumer 1Kc 2cm, ...) si ze slabsiho oloupaneho proutku snadno zhotovite pravitko dlouhe 50 cm nebo i cely metr a s jeho pomoci bude jednoduche si poridit z lana nebo provazku " pasmo" k mereni vetsich delek.
Urcovani vzdalenosti sirkovou metodou bude vsak i pri teto presnosti zaviset do znacne miry na nasem subjektivnim odhadu. Presto s ni vetsinou vystacime, protoze pri vetsich vzdalenostech nevyzadujeme obvykle zvlastni presnost. Mensi vzdalenosti a rozmery ruznych terennich predmetu muzeme urcovat daleko presneji. Nebo se vam snad zda, ze je to zbytecne, kdyz uz jsme si poridili docela presna meridla a muzeme si vsechno zmerit " na centimetr "? Vzdycky to totiz nepujde. Ci snad polezete na vrcholek stromu nebo poplavete s cejchovanym provazkem pres reku, budete-li si chtit zmerit jeho vysku nebo jeji sirku? Neni to treba - jen zase vedet jak na to.
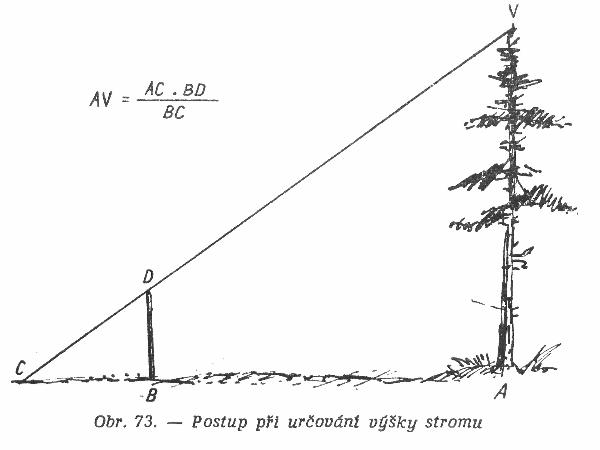
Vysku stromu (veze, kominu apod.) zmerime takto : odmerime od paty stromu (A) urcitou vzdalenost a v teto vzdalenosti (B) zarazime tyc 1 m vysokou (viz obr.) ( obr.73).
|
 |
|
Polozime se na zem tak daleko za tyc, aby se nam jeji vrchol (D) kryl s vrcholem stromu (V). Bod, z nehoz se divame, oznacime nejakym predmetem (C). Vzdalenost CB opet zmerime. Vynasobime-li nyni vzdalenosti AC a BD a vysledek delime vzdalenosti BC, vyjde nam vyska stromu.Napriklad: zarazili jsme tyc 1m vysokou ve vzdalenosti 20m od paty stromu. aby se nam jeji vrchol kryl s vrcholem stromu, museli jsme se polozit 4metry za tyc, Nasobime tedy 24x1=24, deleno ctyrmi je sest. To znamena, ze strom je vysoky sest metru.Vida slo to i bez splhani na vrcholek stromu.
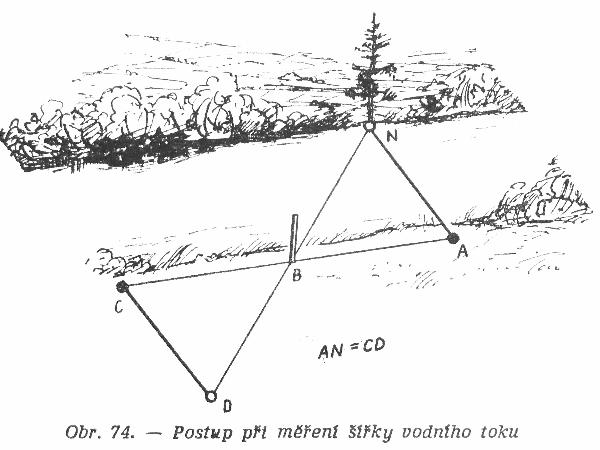
Stejne to pujde i s merenim sirky reky bez lodky a plavani. Jen zpusob bude trochu jiny: vyhledame si tesne u brehu na druhe strane reky nejaky predmet (vetsi kamen, parez, strom, ker) a postavime se na sve strane - take co nejblize k vode- primo proti tomuto predmetu (N). Misto vlastniho stanoviste si oznacime A (obr.74).
|
|
Z tohoto mista pujdeme rovne, tesne podel brehu a odpocitame urcity pocet kroku, napriklad 50 (na obrázku bod B ).Do tohoto bodu zarazime tyc a ujdeme stejnym smerem podel brehu dalsich 50kroku (bod C) V bode C se obratime v pravem uhlu a pujdeme smerem od reky tak dlouho, az se tyc v bode B bude kryt s predmetem N na druhe strane reky. Toto misto si oznacime D . Ziskali jsme tak dva presne stejne pravouhle trojuhelniky a to znamena ze vzdalenost AN se rovna vzdalenosti DC. Staci jiz jen zmerit delku DC - na suchu uz to pujde bez obtizi! Inu chytrost nejsou zadne cary a hlavni je, ze si clovek vi vzdycky rady.
Tolik ze Zalesacke prirucky p.Marase a p.Breziny.
|
 |
|
A jak najit cache ?
Zkuste se naucit odmerovani vysky, treba podle Zalesacke prirucky a zjitete na uvodnich souradnicich vysku brizy. Nejvyssi ze tri briz pobliz uvodnich souradnic.
Rozhodne nedoporucuji lezt po strome !!!
Mala napoveda : Kdyz si prohlednete kmen, ve vysce ctrnacti metru je oranzovy pasek. Tim si muzete "zkalibrovat" sva mereni. Trojuhelniky jsou pravouhle a vy stojite v mirnem svahu, tak si nemusite lehat. Vysku brizy zaokrouhlete na cele metry vyjde vam cislo A. Neprolézejte krovi, stací se sehnout na cesticce.
N 49° 40.( 414 - 1.5*A ) E 14° 00.( 420 +2*A )
Kdyby vám cache vyšla dál než 150 metrů, tak je něco špatně.
Preji prijemnou zabavu a dobre oko.
|