Přijďte s námi oslavit Den čísla π!
Proč právě tento den? Dle amerického zápisu je 14. března 2015 3/14/15. Většina lidí ví, že π je 3,14, menší počet lidí ví, že π je 3,1415. Naše oslava ale bude ultimátní oslavou, protože budeme slavit v 9:26:54. Přesněji 3/14/15 9:26:54, čímž datum a čas vytvoří číslo π s přesností až na 9 desetinných míst. Tato příležitost nebude opakovat další 100 let.
A pro zajímavost - Albert Einstein se narodil na Pi Day (14. března 1879)
Co je vlastně π?
Geometricky je π definováno jako poměr obvodu kružnice k jejímu průměru. Dale je π je iracionální číslo, což znamená, že ho nelze vyjádřit podílem dvou celých čísel (většina z nás se na základní škole učila, že π je 22/7, tento zlomek se ale od π liší již na třetím desetinném mistě). Je to také transcendentní číslo, což znamená, že neexistuje polynom s racionálními koeficienty, pro který by π bylo kořenem.
Protože π je iracionální číslo, číslice v jeho desetinném rozvoji se nikdy nezačnou opakovat. Sled těchto číslic fascinuje matematiky i laiky a během posledních pár století se vkládají snahy do vypočítání více číslic π a zkoumání jeho vlastností. Zatím se ale nepodařilo najít žádný vzor, podle kterého by se číslice opakovaly.
Jak se π vypočítává?
π se dá odhadnout narýsováním kružnice, změřením jejího průměru a její délky a následným vydělením délky průměrem. Další způsob, který navrhl Archimédés, je spočítat obvod on pravidelného mnohoúhelníku s n stranami s vepsanou kružnicí o průměru d. Potom lze vytvořit limitu posloupnosti, kde se n přibližuje nekonečnu:

Čím více má mnohoúhelník stran, tím menší je jeho největší vzdálenost od kružnice. Archimédés určil přesnost tohoto způsobu porovnáním obvodu mnohoúhelníku opsaného kružnici s obvodem mnohoúhelníku se stejným počtem stran vepsaného kružnici. S použitím mnohoúhelníku s 96 stranami spočítal rozsah, v kterém π leží:

Na začátku 20. století vymyslel indický matematik Srinivasa Ramanujan několik nových vzorců pro π, z nichž některé jsou pozoruhodné svou elegancí, hloubkou a rychlostí konvergence. Jeden z jeho vzorců je řada
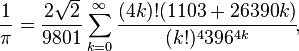
kde k! je faktoriál k, jímž se podařilo prolomit hodnotu 1 miliardy desetinných čísel. Současný rekord pochází z roku 2010 a činí přes 5 bilionů desetinných čísel.
Na různých internetových stránkách se vyskytuje mnohem více číslic čísla π. I když bylo π spočítáno na více než bilion (1012) číslic, v aplikované matematice se většinou používá zaokrouhlení pouze na několik desítek desetinných míst. 11 desetinných míst π například stačí na odhad délky kružnice, která je velká jako Země, s chybou menší než jeden milimetr, a 39 desetinných míst stačí na jakoukoli představitelnou aplikaci.
Jedna poslední zajímavost: Mějme pizzu o poloměru z a konstantní tloušťce a, její objem bude Pizza
Co nás čeká?
Tradiční geocaching flashmob - sejdeme se na souřadnicích v 9:15, v 9:26:54 uděláme společnou fotografii a v 9:30 se rozejdeme.
Jelikož se jedná o Pi Day, měli by být všichni účastníci viditelně označeni touto matematickou konstantou. Její grafickou podobu nechám na každém z vás, může to být prosté π, či jeho geometrická podoba, nebo i jiné provedení.
Budou CWG?
Ano, zájem pište do logů.
