Fibonacciho čísla
Fibonacciho čísla tvoří jednu z nejslavnějších posloupností pojmenovanou po Leonardu Pisánském neboli Fibonaccim. Jedná se o nekonečnou posloupnost přirozených čísel, kde každé číslo je součtem dvou předchozích, počínaje 0 a 1, tj.
F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2) pro n>1
Posloupnost tedy začíná následovně:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, ...
Fibonacciho čísla dosahují velmi rychle vysokých hodnot, což je vidět na následujícím grafu.
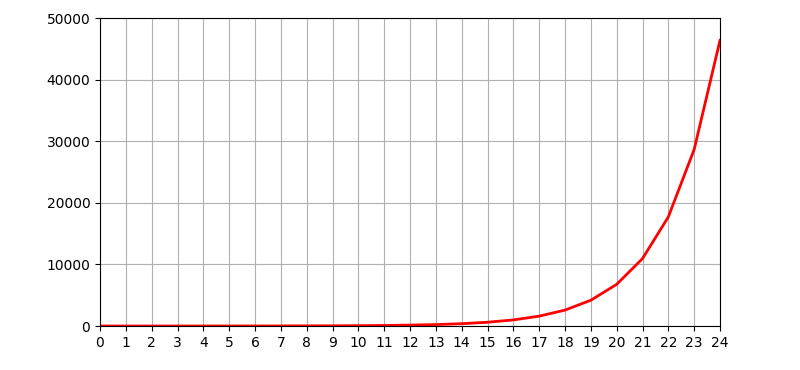
Např. pro čísla 15, 150 a 1500 obdržíme hodnoty:
F(15) = 610 (3 místa)
F(150) = 9969216677189303386214405760200 (31 míst)
F(1500) = 135511256685631...122583354898000 (314 míst)
Fibonacciho čísla mají úzký vztah ke zlatému řezu, jehož hodnota je
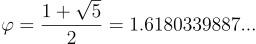
Vzájemné poměry dvojic po sobě jdoucích Fibonacciho čísel, tedy zlomky 2/1, 3/2, 5/3, 8/5, 13/8, 21/13 atd. se postupně s rostoucím n blíží ke zlatému řezu. Jinak řečeno posloupnost F(n+1) / F(n) má pro n jdoucí k nekonečnu limitu rovnou φ.
Kde hledat keš
Keš se nachází na souřadnicích:
N nn° nn.nnn', E ee° ee.eee'
Souřadnice N jsou prvních 7 číslic Fibonacciho čísla, které má celkem 1224418 číslic, tj.
N: F(n) = nnnnnnnxxx...xxx (1224418 míst)
Souřadnice E jsou posledních 7 číslic jiného velkého Fibonacciho čísla F(n), kde
n = 16180339887498948482045868343656381177203091798057628621354486227052604628189024497072072041893911374848290908
tj.
E: F(161...908) = xxx...xxxeeeeeee
Výpočty se mohou zdát náročné, ale využijete-li specifických vlastností Fibonacciho posloupnosti, sami uvidíte, že to tak hrozné není. A ujišťuji vás, že nemusíte nic programovat.

