This is another in my series of advanced sudoku strategies. I originally wanted to arrange these caches so that you actually have to understand and use the technique and not simply throw it into a solver. However, *some* people seem to interpret this statement as a challenge. I have come to terms with the idea that I am not teaching these people anything. Instead I am improving the quality of their auto-solving programs. I guess, this series is having some benefit after all.
Swordfish is the next step up from X-Wing. Whereas X-Wing is based on the principle of doubles, Swordfish is based on triples. Remember that the X-Wing position exists when a single digit must belong in one of two rows such that the only possibilities form the corners of a rectangle. See my X-Wing puzzle if you don't remember. A Swordfish position exists when a single number exists in one of three rows (or columns) such that the only possibilities line up into exactly three columns (or rows). X-Wing is formed from the corners of a 4-point rectangle. Swordfish is formed from the corners, midpoints, and center of a 3 x 3 rectangle.
Don't start looking for Swordfish until you can do X-Wings. When you are working with doubles, there are only two combinations. When you are working with triples, however, there are six combinations. They are not easy to spot and not easy to keep in your head.
The image below shows the "classic" Swordfish position, based on the digit 5. Note that the 5 is limited to the three rows (red arrows) such that it is also lined up in three columns (blue arrows). This pattern ensures that the 5 in those columns can only appear in the yellow squares. Thus the green squares cannot contain a 5. I could have constructed a similar pattern with the 5 restricted to three columns, lined up in three rows. Note that this is a stairstep pattern.
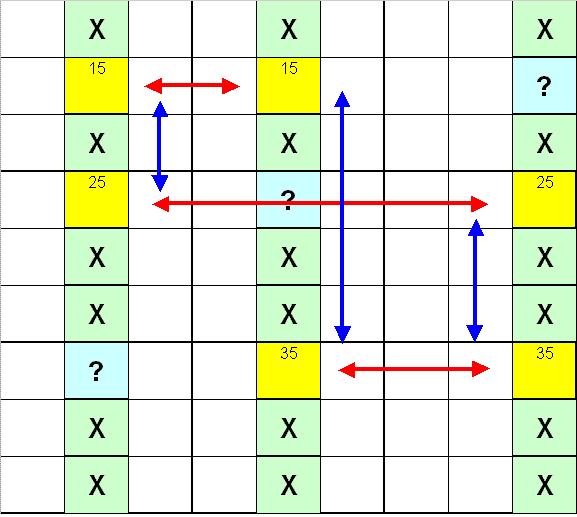
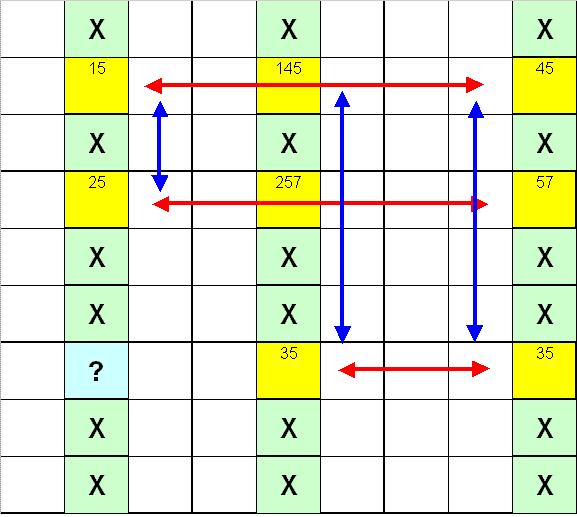
If you are paying attention, you probably want to ask me about the blue squares with the question marks. If a 5 appears in these squares, they cannot be eliminated as they form part of the 3 x 3 rectangle. That situation is impossible in the exact diagram shown above, but it is easy enough to construct a teaching diagram where it does (see below). The "classic" position consists of three sets of doubles filling out two rows/columns in the 3 x 3 rectangle. It is probable that when you do find your first Swordfish on your own (and a thrilling moment that will be!) that it will follow the classic pattern. However, the contraint is based on the 3 x 3 rectangle and it is possible that one, two, or even all three rows may have the key digit.
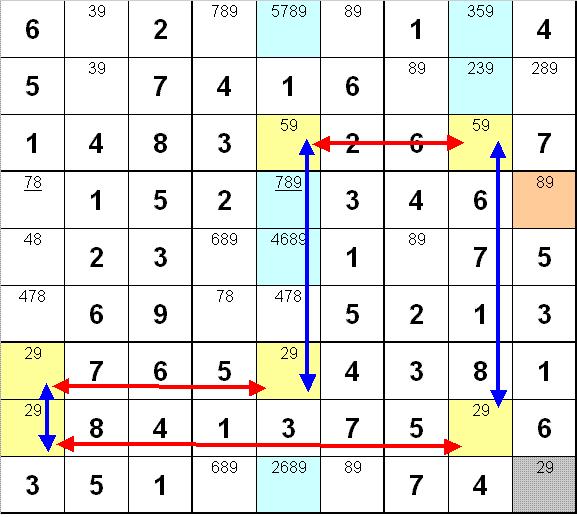
Here is a complete puzzle adapted from Sudopedia. Notice that the yellow squares are the only possibilities in their rows where a 9 can exist (red arrows). These squares are lined up in three columns (blue arrows). This pattern ensures that a 9 cannot exist anywhere else in those columns. You can then remove the 9s from the blue squares. Once you do that, note the blue cell with the underlined 789 . Aftere the 9 is eliminated, you are left with only 78. This pairs up with the underlined 78 in the same row, meaning that the tan square must contain a 9. The gray square must then contain a 2 and the rest of the puzzle falls apart after that.
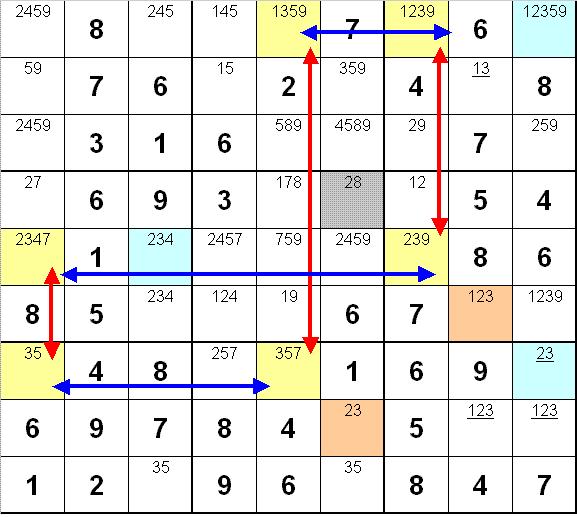
Here is another example adapted from Sudopedia based on columns instead of rows. Note that the yellow cells are the only places in their column where a 3 can exist (red arrows). These cells line up in three rows (blue arrows). Therefore the blue squares cannot contain a 3. Note the blue square with the underlined 23. This square now must contain a 2, allowing you to eliminate a 2 from the underlined 123 cells in the same 3x3 box. Not only does this leave you with a 1-3 pair but one of them also pairs with another 1-3 above it in the same column (8th column). Because these are pairs, the tan squares cannot contain a 1 or a 3. They must therefore both contain a 2. The gray cell must now contain an 8, and the puzzle falls apart after that.
Here are the ingredients for spotting a Swordfish.
1. A single digit must be restricted to TWO or THREE cells in a row (or column).
2. There must be exactly THREE rows (or columns) such that...
3. These cells must line up in exaclty THREE columns (or rows).
4. To put it more clearly: The pattern of these cells must form a 3 x 3 rectangle.
Note: Either rows or the columns must constrict the digit to the pattern. The other dimension will then form the basis for eliminating digits from the rest of the puzzle. In the examples above, I have shown the constricted element by red arrows. The blue arrows indicate the other dimension.
[Email me if this doesn't make sense.]
Supposedly the name comes from the classic position's similarity in shape to a swordfish's "sword." That story seems to be apocraphal. If true, I would have expected the name to be "Sawfish" instead. However, it does serve as a memory trigger when you go looking for the pattern.
Now for the puzzle! The Sudokus below each have a Swordfish apparent relatively quickly. In fact, you will need to use the Swordfish after filling in only a few cells or you won't be able to solve the Sudoku at all. (Please don't interpret that statement as a challenge.) Every Swordfish depends on a single digit. In the first two examples above, the digit is a 5. In the first complete puzzle, the digit is a 9. In the second complete puzzle, the digit is a 3. Let this digit in the first Sudoku below be X. Let this digit in the second Sudoku below be Y. Then the cache is at N 37 33.ABC W 122 18.DEF. Use the following formulas. If the calculations for B, D, E and F result in a multi-digit number, take the final digit. (That's how I mix things up.) Note that the caret ^ refers to exponential power. Also note that I may have the used the same digit in each puzzle. (i.e. X may equal Y, or it may not.)
A = X
B = 2Y
C = Y
D = X + Y
E = 3Y - X
F = (X - Y) ^ 4 [i.e. first subtract Y from X and then take the result to the 4th power; alternatively you can square the remainder and then square that result.]
Both of these Sudokus are adapted from Sudopedia. They are rather pedestrian other than the Swordfish. Usually you find a Swordfish near the end of a puzzle, and the experience is exciting. ("I found a Swordfish!!! I'm a master puzzler!!! Woo-Hoo!!" And all that.) These, of course, are teaching examples.
Here is the first Sudoku. The first thing you will do is to fill in all of the instances of one digit. At that point, you're pretty much helpless unless you can find the Swordfish. At that point, you will fill in a single digit, and the puzzle will practically solve itself. This Sudoku will yield the X digit.

Here is the second. You will fill in about six digits, at which point you will come to a crashing halt. I think there are a couple of minor things you can do at that point, but unless you find the Swordfish, you're out of luck. At this point, you will fill in a single digit, but have some figuring to do to solve the rest of the puzzle. However, you wont have to do anything harder than doubles and triples. Remember that this Sudoku will yield the Y digit.
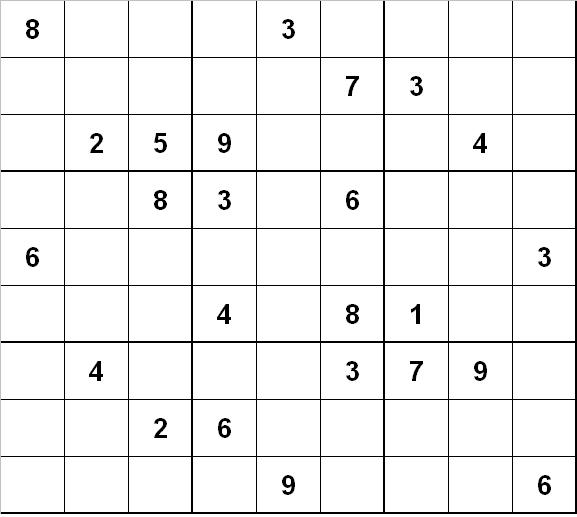
Please remember that I am not doing anything tricky here, although the description may be convoluted and dense. If anythiing is unclear, please let me know. I chose these Sudokus because as nearly as I can tell, you have to use Swordfish to solve them.
One note of caution. One of the intriguing things about Sudoku is that there is often more than one way to solve them. You may use methods that will let you solve these puzzles without using a Swordfish. If so, you have my respect, but you don't have my cache. You have to find a Swordfish in these Sudokus to find the cache. [After doing further analysis, I noticed that you can do the first puzzle without resorting to Swordfish by doing about 4 successive Finned X-Wings. I am going to assume that my audience at this point in their careers will be able to find Swordfish easier than Finned X-Wing, but the Puzzling Crowd is nothing if not creative, resourceful, and contrary. I repeat: To find the cache you must find the Swordfish.]
I fiddled with these diagrams and solved them six-ways-to-Sunday, but I may have missed something. It has happened before. If you notice a mistake or ambiguity, please just send me a gentle note and I'll get things fixed. Happy Puzzling, and thank you for doing my caches!
Note to the curious and/or mathematically inclined: X-Wing and Swordfish belong to a family known collectively as "Fish Techniques" or some such designation. I have no idea why the image of a fish has been used (the Swordfish etymology described above nothwithstanding). However you can think of X-Wing as the technique in 2 dimensions. Swordfish is the 3-dimensional version. You might suppose that we can do this same sort of thing in 4 or more dimensions. You would suppose right. The 4-dimensional version, based on a 4 x 4 rectangle is called Jellyfish. The 5-dimensional version is called Squirm Bag. Obviously the Sudoku Crowd has a distinctly odd sense of imagery. (Actually, it gets odder. All of the fish also have "finned," "sashimi," and "kraken" forms.)
By the time someone tried to construct a 6-dimensional puzzle, the Crowd realized that 5 dimensions and up are unnecessary. (Mathematicians love reducing problems to the most basic example.) Given the 9 x 9 Sudoku grid, a 5 x 5 pattern is really a 4 x 4 pattern looked at from the other direction. (You can also think of it as positive versus negative space.) Thus any Squirm Bag is really a Jellyfish (or Swordfish or X-Wing depending on the known digits) in disguise. All of this is really academic. You probably won't have to go looking for anything higher than a Swordfish. I've found a total of two Jellyfish in all the puzzles I have done. I have a feeling these puzzles could have been solved more easily by other methods. Yet, I did find the Jellyfish, and it doesn't make sense to go looking for alternate methods of solving once you've figured out a valid one.
I have a Jellyfish example in the gallery, if you wish to try your hand at finding one. It is adapted from Sudopedia. I haven't examined it extensively, but it does yield a Jellyfish. Email me if you have issues with it.